 |
|
. . |
Physik für Schülerinnen und Schüler Die Zukunft vorhersagen - Kausalität © H. Hübel Würzburg 2013 |
Empfohlene Glossarthemen: |
Impres-sum |
Kausalität bedeutet in der Mechanik:
Aus bekannten Anfangsbedingungen
x0 und v0 ergibt sich
|
Das ist also das Programm der Newtonschen Mechanik und die eigentliche Aussage im 2. NG. Aus ihr ergibt sich die Möglichkeit "die Zukunft vorherzusagen", wenigstens dort, wo Kausalität anwendbar ist. Dieses Programm heißt auch "schwache Kausalität" im Unterschied zur "starken Kausalität". Bei der schwachen Kausalität werden exakte Anfangsbedingungen vorausgesetzt, die dann zu bestimmten exakten Wirkungen führen.
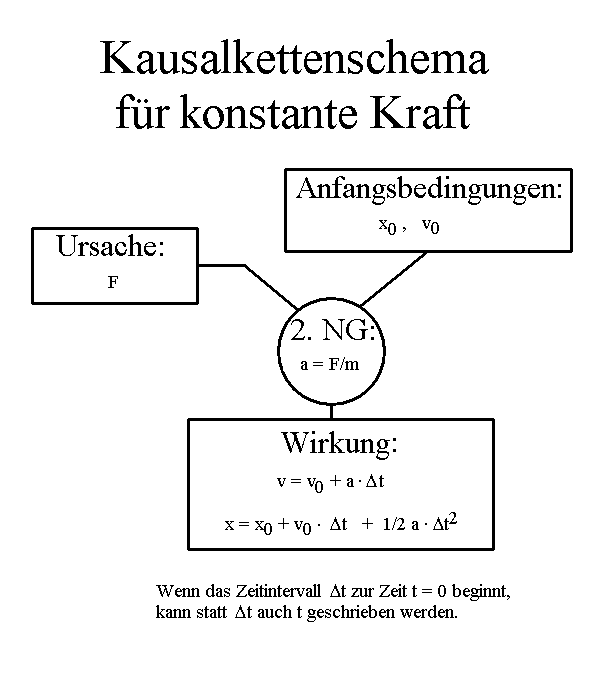
Wie Kausalität angewendet wird, ergibt sich für eine konstante Beschleunigung in einem Zeitintervall Δt nach folgendem Schema (das manchmal PUB = Prinzip der Unabhängigkeit der Bewegungen genannt wird):
| PUB | . | glf. Bewegung mit v0 | einfache *) glm. beschl. Bewegung mit Beschleunigung a |
| x = | x0 + | v0·Δt + | 1/2·a·Δt 2 |
| v = | . | v0 + | a·Δt |
| a = | . | . | konst. |
*) mit einfachen Anfangsbedingungen (Start aus Ruhe am Koordinatenursprung)
Der Kausalitätsbegriff ist nicht in allen Fällen anwendbar. Einschränkungen gibt es in der Quantenphysik, bei makroskopischen Systemen aus sehr vielen Teilchen und bei komplexeren, speziell nichtlinearen Systemen sogar in der klassischen Mechanik (vgl. "Chaostheorie").
Für konstante Kraft auf ein klassisches Teilchen bzw. eine gleichmäßig beschleunigte Bewegung wird also Kausalität beschrieben durch das folgende Kausalkettenschema (es kann vektoriell oder eindimensional für eine Koordinate der entsprechenden Vektoren gesehen werden):
 |
Bei zeitlich veränderlicher Kraft muss man sich auf kleine Zeitabschnitte Δt beschränken, in denen F bzw. a in guter Näherung konstant sind. Am Ende dieses Zeitabschnitts erhält man dann in guter Näherung Geschwindigkeit v und Ort x. An ein solches Intervall muss sich dann das nächste anschließen mit Anfangsbedingungen, die sich aus den momentan erreichten Werten für x und v ergeben. Die geänderten Werte x0 und v0 bestimmen evtl. eine geänderte Kraft F, die wiederum zu einer geänderten Beschleunigung a führt u.s.w. Das ist die "Methode der kleinen Schritte". Beachte den Hinweis für eine gleichwertige andere Schreibweise von Δx *)
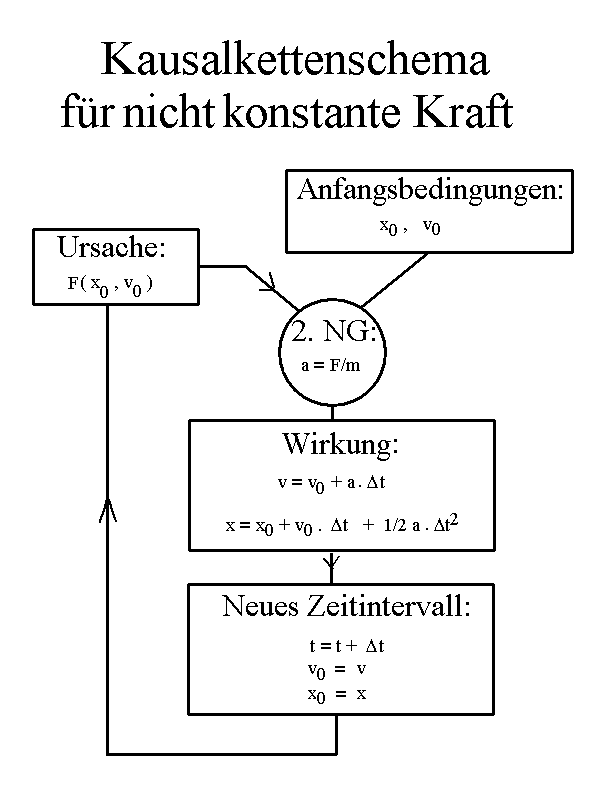 |
Ein bestimmter Zeitschritt liefert also v und x. Für das nächste Zeitintervall wird v als Anfangsgeschwindigkeit v0 gewählt und x als Anfangsorts x0 (Rückwärtspfeil). Dann beginnt der nächste Schritt nach dem gleichen Schema.
Die "Methode der kleinen Schritte (MdkS)" kann per Hand bzw. Taschnerechner, mit PC-Programmen und mit Tabellenkalkulationsprogrammen wie EXCEL vollzogen werden. Für eine Federschwingung mit der Kraft F = - D·x (Federhärte D) müsste dann eine Tabelle nach folgendem Muster ausgefüllt werden:
Anfangssituation:
| Δt = 0,1 s m = 1 kg D = 1 N/m | |||||||
| v0 | x0 | F = - D·x0 | a = F/m | Δv = a·Δt | v = v0 + Δv | Δx | x = x0 + Δx |
| 10 | 0,0 | ... | ... | ... | ... | ... | ... |
| ..... | ... | ... | ... | ... | ... | ... | ... |
| ... | ... | ... | ... | ... | ... | ... | ... |
1. Schritt:
| Δt = 0,1 s m = 1 kg D = 1 N/m | |||||||
| v0 | x0 | F = - D·x0 | a = F/m | Δv = a·Δt | v = v0 + Δv | Δx | x = x0 + Δx |
| 10 | 0,0 | 0 | 0 | 0 | 10,0 | 1,0 | 1,0 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| ... | ... | ... | ... | ... | ... | ... | ... |
Beginn des 2. Schritts:
| Δt = 0,1 s m = 1 kg D = 1 N/m | |||||||
| v0 | x0 | F = - D·x0 | a = F/m | Δv = a·Δt | v = v0 + Δv | Δx | x = x0 + Δx |
| 10 | 0,0 | 0 | 0 | 0 | 10,0 | 1,0 | 1,0 |
| 10,0 | 1,0 | -1,0 | -1,0 | -0,10 | ... | ... | ... |
| ... | ... | ... | ... | ... | ... | ... | ... |
usw., von Schritt zu Schritt.
Für Δx wird entweder Δx = v0·Δt + 1/2a · Δt2 oder gleichwertig Δx = 1/2 · (v0 + v)·Δt verwendet.
Eine Möglichkeit besteht z.B. darin, dass du die ersten zwei Zeilen dieser Tabelle mit der Hand bzw. mit Taschenrechner ausrechnest und alle weiteren Zeilen mit dem PC. Ein Ergebnis zeigt die folgende Abbildung:
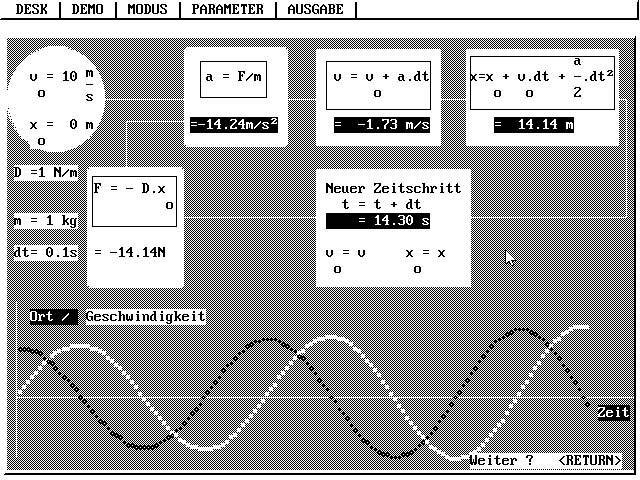 |
Mit Programm KAUSALIT erzeugtes Bildschirmbild. Nach
jedem Tastendruck erscheint ein weiterer Schritt auf dem
Bildschirm.
Schließlich ergibt sich so etwas wie eine Sinuslinie für den Ort und eine Cosinuslinie für die Geschwindigkeit: Die Kraft F = - D·x führt zu einer "harmonischen Schwingung". Die leichte Vergrößerung der Amplitude weist darauf hin, dass man die Schrittweite Δt verkleinern sollte. |
Falls das Ergebnis nicht genau genug ist, hilft es häufig, die Schrittweite Δt zu verkleinern.
Die Methode der kleinen Schritte ist als Rechenverfahren nicht so interessant. Es gibt noch genauere Varianten. Die Kernaussage ist vielmehr, dass sie ein Hilfsmittel ist, um mit dem 2. Gesetz von Newton die Zukunft einer Bewegung vorherzusagen. Das ist die Hauptaufgabe des 2. Gesetzes von Newton.
Wegen der Kausalität nenne ich das 2. NG häufig das "Prophetie-Gesetz der Mechanik", weil es erlaubt, bei bekannten Anfangsbedingungen und bekannter Kraft eine Bewegung für alle Zukunft vorherzusagen (wenigstens im Prinzip).
Von Kausalität zu unterscheiden ist Determiniertheit, was so viel wie "Vorherbestimmtheit" bedeutet. Für ein determiniertes System ist die Zukunft durch den Anfangszustand festgelegt und damit für alle Zeiten (solange sich das System nicht ändert) vorherbestimmt. In der Physik bedeutet Determiniertheit, dass sich ein System nach Ursache und Wirkung beschreiben lässt (Kausalität), dass sich aus Anfangsbedingungen spätere Zustände vorherberechnen lassen (Vorherberechenbarkeit als Folge der Kausalität. Wie das geschieht, hat für die Mechanik Newton gezeigt), aber dass zusätzlich das Ergebnis dieser Rechnung mit der Realität übereinstimmt.
|
"Vorhersagbarkeit = Vorherberechenbarkeit
+ Übereinstimmung der Vorhersage mit der Realität"
Wie Newton gefunden hat, lässt sich für ein klassisches System aus wenigen Teilchen bei bekannten Anfangsbedingungen und bekannten Kräften die Zukunft vorherberechnen. In der Praxis sind aber Anfangsbedingungen nie exakt bekannt. In vielen Fällen führen erfreulicherweise ähnliche Anfangsbedingungen zu ähnlichen Wirkungen (starke Kausalität). Deshalb ist Newtons Programm auch für solche Situationen wichtig. In der Quantenphysik fehlt prinzipiell die Vorherberechenbarkeit von Mikroteilchen, weil diese nie alle klassisch denkbaren Eigenschaften gleichzeitig besitzen (Kausalität nicht anwendbar). In großen (makroskopischen) Systemen fehlt die Vorherberechenbarkeit auf mikroskopischer Ebene, weil die Anfangsbedingungen aller beitragenden Teilchen wegen ihrer großen Zahl aus praktischen Gründen nicht ermittelt werden können (Laplace hat unrecht). Klassische chaotische Systeme lassen sich zwar vorherberechnen. Was die Rechnung aber mit der Realität zu tun hat, ist offen, da die Anfangsbedingungen aus praktischen Gründen nie exakt ermittelt werden können. |
| . |
behauptet Kausalität ? |
Vorherberechenbarkeit |
Übereinstimmung der Vorhersage mit der Realität |
Lässt sich die Zukunft vorhersagen? |
|
Newton (17. Jhdt.)
|
ja |
für Systeme aus wenigen Körpern (max. 2) |
bei Systemen aus wenigen Körpern |
ja, aber nur für Systeme aus wenigen Körpern, wenn ähnliche Anfangsbedingungen zu ähnlichen Wirkungen führen ("starke Kausalität") |
|
Laplace (18. Jhdt.)
|
ja: Die Welt mit allem, was in ihr ist, ist wie ein Uhrwerk, das einmal angestoßen wurde. Alles verläuft vermeintlich vorherbestimmt. |
im Prinzip für alle Systeme; erfordert aber evtl. "Laplaceschen Dämon" (Supercomputer), der alle Rechungen durchführen kann |
praktisch nur erreichbar für kleine Systeme aus wenigen Körpern; In Realität lassen sich nur von wenigen Körpern die Anfangsbedingungen genau kennen und die Rechnungen durchführen. |
In Realität wie oben. Bei größeren Systemen ist es praktisch unmöglich, alle Anfangsbedingungen zu kennen und die komplexen Rechnungen durchzuführen. |
|
Physik chaotischer Systeme (20.
Jhdt.)
|
ja |
ja, für Systeme aus wenigen Körpern ("deterministisches Chaos") |
Wegen ungenau bekannter Anfangsbedingungen haben Berechnungen evtl. nichts mit der Realität zu tun. |
bestenfalls für kurze Zeit; ähnliche Anfangsbedingungen führen eventuell zu weit abweichenden Wirkungen |
|
Quantenphysik (20. Jhdt.)
|
Für Mikroteilchen nicht anwendbar: Kein Mikroteilchen kann zugleich Ort und Geschwindigkeit als Eigenschaften haben |
nein; nur für Wahrscheinlichkeiten |
. |
nein; für Mikroteilchen prinzipiell unmöglich nur Wahrscheinlichkeiten für zukünftig eintretende Messwerte lassen sich vorhersagen |
| schwache Kausalität | Exakte Anfangsbedingungen führen zu exakten Wirkungen. |
| starke Kausalität | Ähnliche Anfangsbedingungen führen zu ähnlichen Wirkungen. |
| deterministisches Chaos | Ähnliche Anfangsbedingungen führen evtl. zu stark abweichenden Wirkungen. |
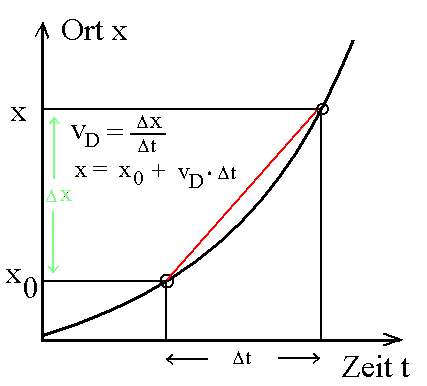 |
Wenn du die Durchschnittsgeschwindigkeit vD im
Zeitabschnitt Δt
kennst, weißt du, wie du vom Anfangsort x0 zum Ort
x am Ende des Zeitabschnitts kommst (rote Strecke):
x = x0 + vD·Δt Ein naheliegender, aber leider nicht immer richtiger Ansatz für vD ist: vD = 1/2 · ( v0 + v ) Wenn v0 die Geschwindigkeit zu Beginn des Zeitabschnitts und v die Geschwindigkeit am Ende des Zeitabschnitts ist. (v = v0 + a·Δt) |
Es gibt eine Möglichkeit, das Kausalkettenschema mathematisch einfacher als im Flussdiagramm oben, aber physikalisch gleichwertig, zu schreiben. Gehe von einer konstanten Beschleunigung a aus:
Zu Beginn eines Zeitintervalls Δt sei die Geschwindigkeit v0, am Ende ist sie also v = v0 + a·Δt.
Wenn der Ort zu Beginn des Zeitintervalls Δt x0 ist, dann ist er am Ende x = x0 + v0·Δt + 1/2a · Δt2.
Aus der Ortsänderung Δx = v0·Δt + 1/2a · Δt2 ergibt sich die Durchschnittsgeschwindigkeit vD = Δx/Δt = v0 + 1/2 ·a·Δt = 1/2 ( v0 + v ).
(Das war der naheliegende Ansatz. Wir wissen jetzt, dass er nur für konstante Beschleunigung a gilt. Vielleicht erinnerst du dich an die 5. Klasse, wo du gelernt hast, dass man Durchschnittsgeschwindigkeiten immer mit vD = Δx/Δt berechnen sollte.)
Also: Statt Δx = v0·Δt + 1/2a · Δt2 kannst du auch schreiben:
|
Δx = vD·Δt wobei: v = v0 + a·Δt vD = 1/2 · ( v0 + v ) |
Der Ansatz der Zeichnung ist damit für konstante Beschleunigung a begründet.
(zurück)