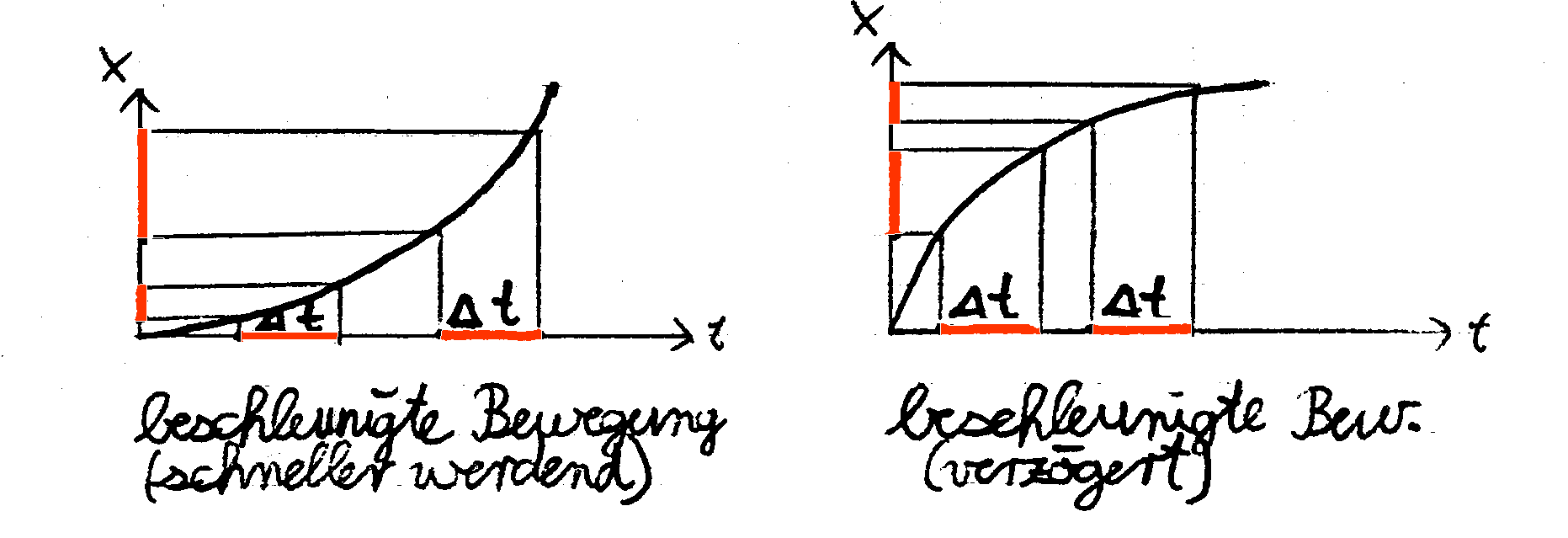
eindimensionale beschleunigte Bewegung (nicht unbedingt gleichmäßig beschleunigt); der Vektorcharakter des Ortsvektors ist durch das Vorzeichen der Ortskoordinate x erfasst; der Anfangsort x0 ist hier jeweils 0, also der Koordinatenursprung.
|
SG041 Gleichmäßig beschleunigte Bewegung ©
H. Hübel Würzburg 2013
|
Eine gleichmäßig beschleunigte Bewegung ist eine Bewegung
mit konstanter Beschleunigung a bzw. unter der Wirkung einer
konstanten Kraft F = m·a . Dabei ist sowohl die Richtung
als auch der Betrag des Beschleunigungsvektors a
und des Kraftvektors F
konstant. Wie in allen Fällen sind Kraft F und Beschleunigung a
gleich gerichtet.
Es liegt nahe, die positive Koordinatenrichtung entsprechend der Bewegungsrichtung zu wählen, wenn eine eindimensionale (lineare) Bewegung vorliegt. Wird der Ort x (die Ortskoordinate) in Abhängigkeit von der Zeit aufgetragen, erkennt man, dass in gleichgroßen Zeitabschnitten Δt ungleich große Ortsänderungen (Verschiebungen) Δx erfolgen.
|
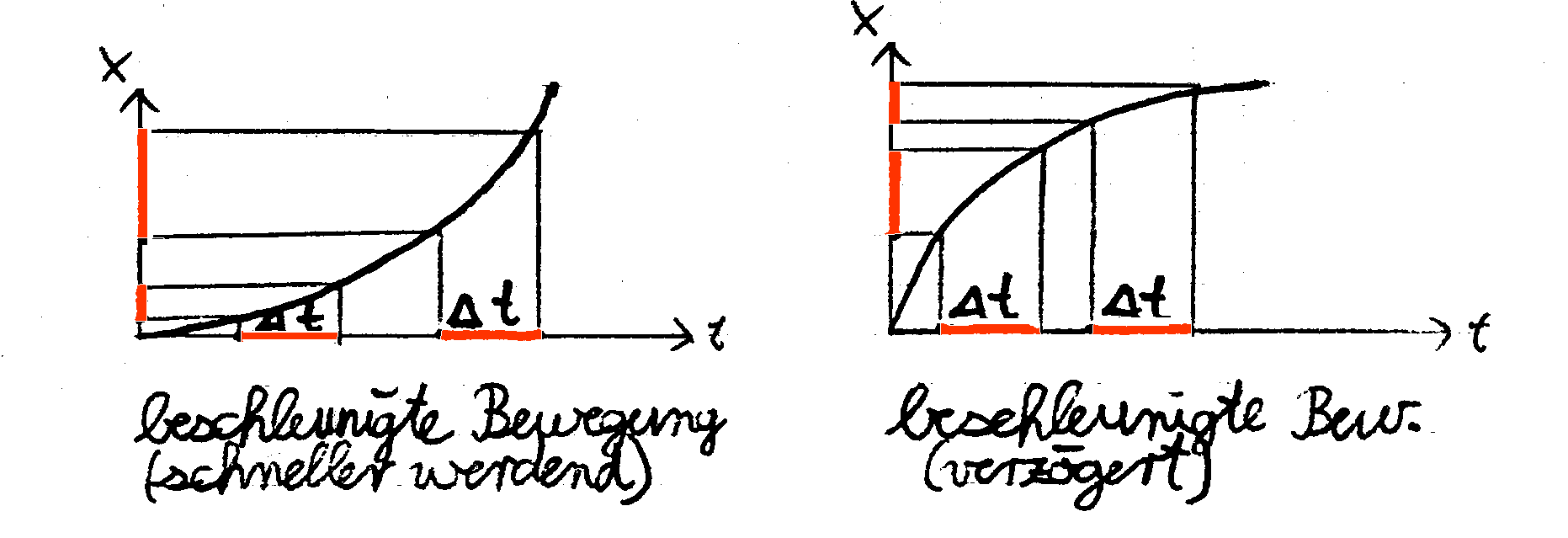Aus einem Schülerheft:
eindimensionale beschleunigte Bewegung (nicht unbedingt gleichmäßig beschleunigt); der Vektorcharakter des Ortsvektors ist durch das Vorzeichen der Ortskoordinate x erfasst; der Anfangsort x0 ist hier jeweils 0, also der Koordinatenursprung. |
Die Registrierung eines t-v-Diagramms für eine gleichmäßig beschleunigte Bewegung zeigt eine lineare Funktion für das t-v-Diagramm mit konstanter Steigung. Das führt zur Definition der Beschleunigung a
| a = Δv/Δt |
Da allgemein (für evtl. sehr kleine Zeitabschnitte Δt)
gilt*)
| (1) x = x0 + v0·Δt
+ ½·a·Δt2
(2) v = v0 + a·Δt |
liegt bei der gleichmäßig beschleunigten Bewegung der Spezialfall vor: Beschleunigung a = konstant (a ≠ 0) für beliebig lange Zeitabschnitte Δt.
Wenn der Zeitabschnitt Δt zur Zeit 0 beginnt, kann man Δt durch t ersetzen:
| (1) x = x0 + v0·t
+ ½·a· t2
(2) v = v0 + a·t |
x0 ist dabei der Anfangsort, v0 die Anfangsgeschwindigkeit. Der t-x-Graph ist eine Parabel. Das t-v-Diagramm zeigt eine Gerade, die eine Ursprungsgerade ist, wenn die Anfangsgeschwindigkeit v0 = 0 ist.
| a ist bei einer linearen Bewegung in jedem Fall die Steigung des t-v-Diagramms. |
Das t-a-Diagramm zeigt eine Konstante. Die "Fläche" unter der t-a-Diagramm entspricht der Geschwindigkeitsänderung Δv = a·Δt . Diese Überlegung ist eine Grundlage des "Flächenverfahrens".
 |
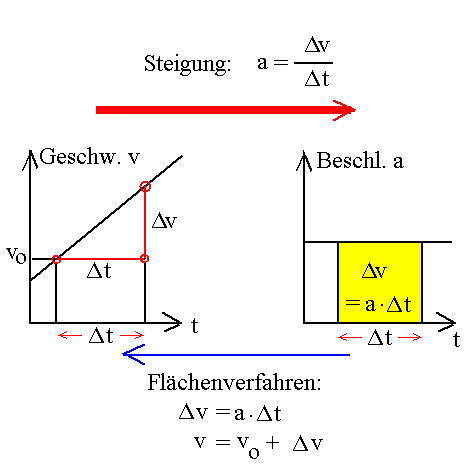Von der Geschwindigkeit v zur Beschleunigung a
mittels der Steigung.
Von der Beschleunigung a zur Geschwindigkeit v mittels des Flächenverfahrens bei bekannter Anfangsgeschwindigkeit v0. |
Bei einer Bewegung im Raum gilt:
| Wegen F = m·a sind die Kraft F und die Beschleunigung a immer gleichgerichtet. |
Die Bewegungsrichtung (Richtung von v) kann eine ganz andere sein, abhängig von der Anfangsgeschwindigkeit v0.
*) Du kannst Dir die Gesetzmäßigkeit sehr leicht merken: Bei Start aus der Ruhe vom Koordinatenursprung aus gilt x = ½·a·Δt2. Bei einer (konstanten) Anfangsgeschwindigkeit v0 kommt noch der Anteil v0·Δt hinzu, also x = v0·Δt + ½·a·Δt2, und bei Start von einem Anfangsort x0 muss dieser noch hinzu addiert werden, also x = x0 + v0·Δt + ½·a·Δt2 . Wie gesagt: Wenn der Zeitabschnitt Δt zur Zeit 0 beginnt, vereinfacht sich die Gesetzmäßigkeit zu x = x0 + v0·t + ½·a·t2.
Die Variante mit Δt ist dann wichtig, wenn eine "gestückelte" Bewegung vorliegt mit unterschiedlichen Bewegungsformen in einzelnen Zeitabschnitten Δt. Dann zählt Δt jeweils vom Beginn eines Abschnitts mit einer veränderten Bewegungsform bis zum betrachteten Zeitpunkt t.
 |
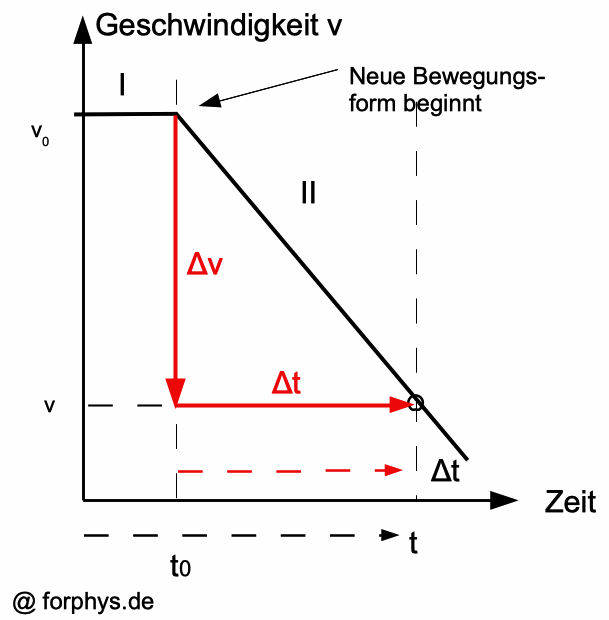Definition von Δt = t - t0
und Δv = v - v0 : Der markierte Punkt hat die Koordinaten (v;t). Er lässt sich auch durch den Zeitabschnitt Δt = t - t0 beschreiben. Δv = v - v0 ist hier negativ, also auch die Beschleunigung a = Δv/Δt. In Abschnitt I gilt: v = v0 = konst. , in Abschnitt II gilt: v = v0 + a·Δt = v0 + a·(t - t0). |
.
( September 2013 )