(1) Von einer ruhenden elektrischen Ladung geht ein elektrisches Feld aus, oder es endet an ihr. Eine bewegte elektrische Ladung erzeugt ein Magnetfeld, sogar, wenn sie sich gleichförmig bewegt. Aber: Jede beschleunigte elektrische Ladung sendet elektromagnetische Wellen aus. Der einfachste Fall sind Elektronen, die in einem gut leitenden Stab hin- und herschwingen, einem so genannten Dipol. Er wird eingesetzt als Sende-Antenne z.B. für den Mobilfunk.

1. Schritt:

Von der bewegten Ladung geht ein elektrisches und ein magnetisches Feld aus. Da sich die Ladung bewegt, sind beide Felder zeitlich veränderlich.

2. Schritt:

Ein zeitlich veränderliches Magnetfeld erzeugt ein elektrisches Wirbelfeld mit geschlossenen Feldlinien. Das besagt das Induktionsgesetz.

3. Schritt:

Ein zeitlich veränderliches elektrisches Feld erzeugt ein magnetisches Feld (Magnetfelder sind immer Wirbelfelder). Das war eine Forderung von Maxwell um 1870 ("Maxwell'sche Ergänzung"), die durch die Entdeckung von elektromagnetischen Wellen durch Heinrich Hertz 1872 bestätigt wurde.

Und so geht das fort. Das magnetische Feld erzeugt ein elektrisches Feld, dieses ein magnetisches, dieses wieder ein elektrisches usw. Nach und nach greifen die Felder immer mehr in den Raum hinaus, zylindersymmetrisch um den schwingenden Dipol herum.

In Wirklichkeit sind die drei Schritte kein zeitliches Nacheinander, sondern laufen parallel zueinander ab.

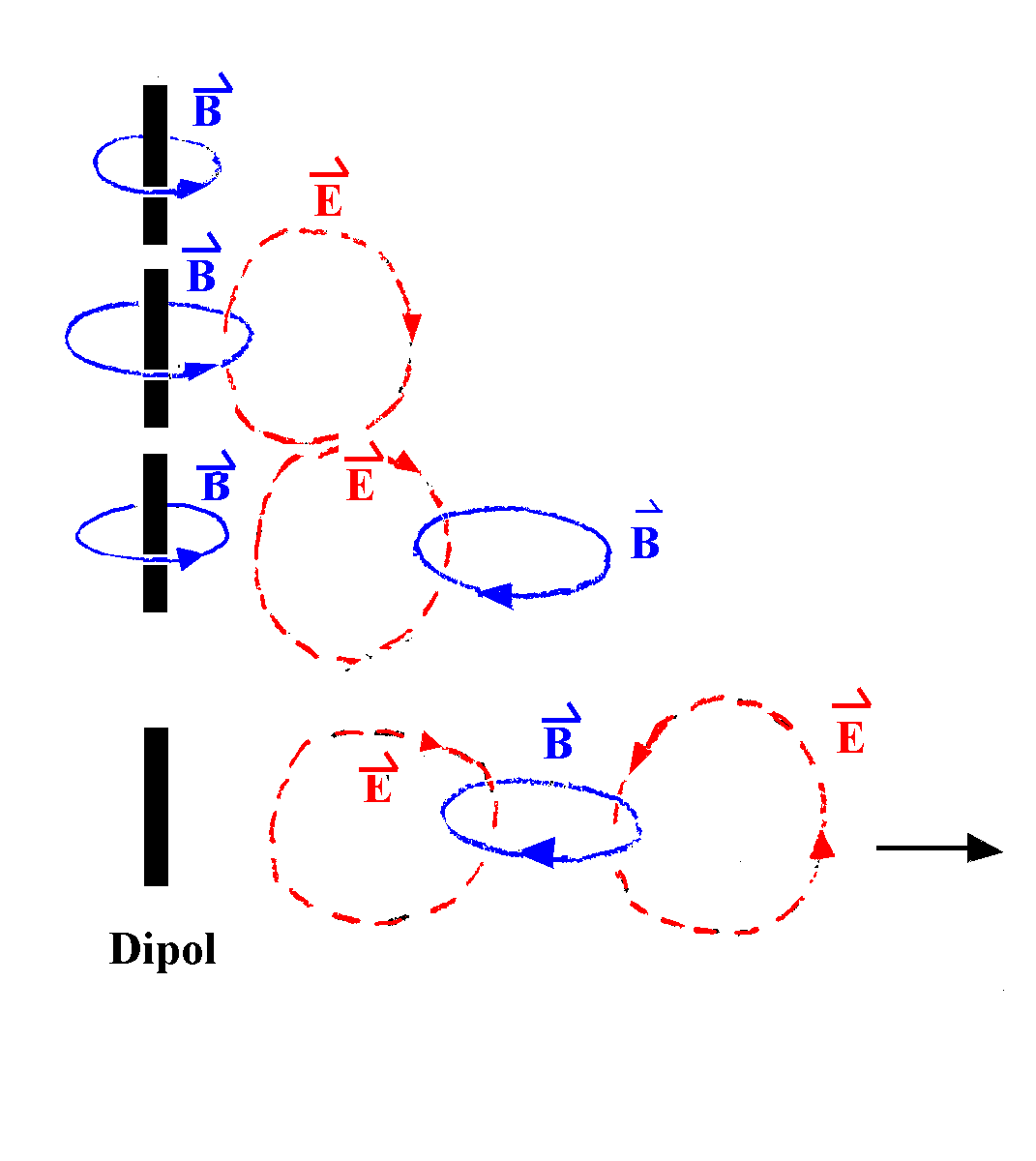Abb. 1 (sehr schematisch): In der Nähe des Dipols (Nahbereich) steckt die abgestrahlte Energie abwechselnd mehr im elektrischen und im magnetischen Feld. Im Fernfeld (Abb. 2) ist eine Phasenverschiebung eingetreten, sodass beide Felder gleichphasig geworden sind. Die Energie steckt dann in beiden Feldern und breitet sich mehr oder weniger radial vom Dipol aus.

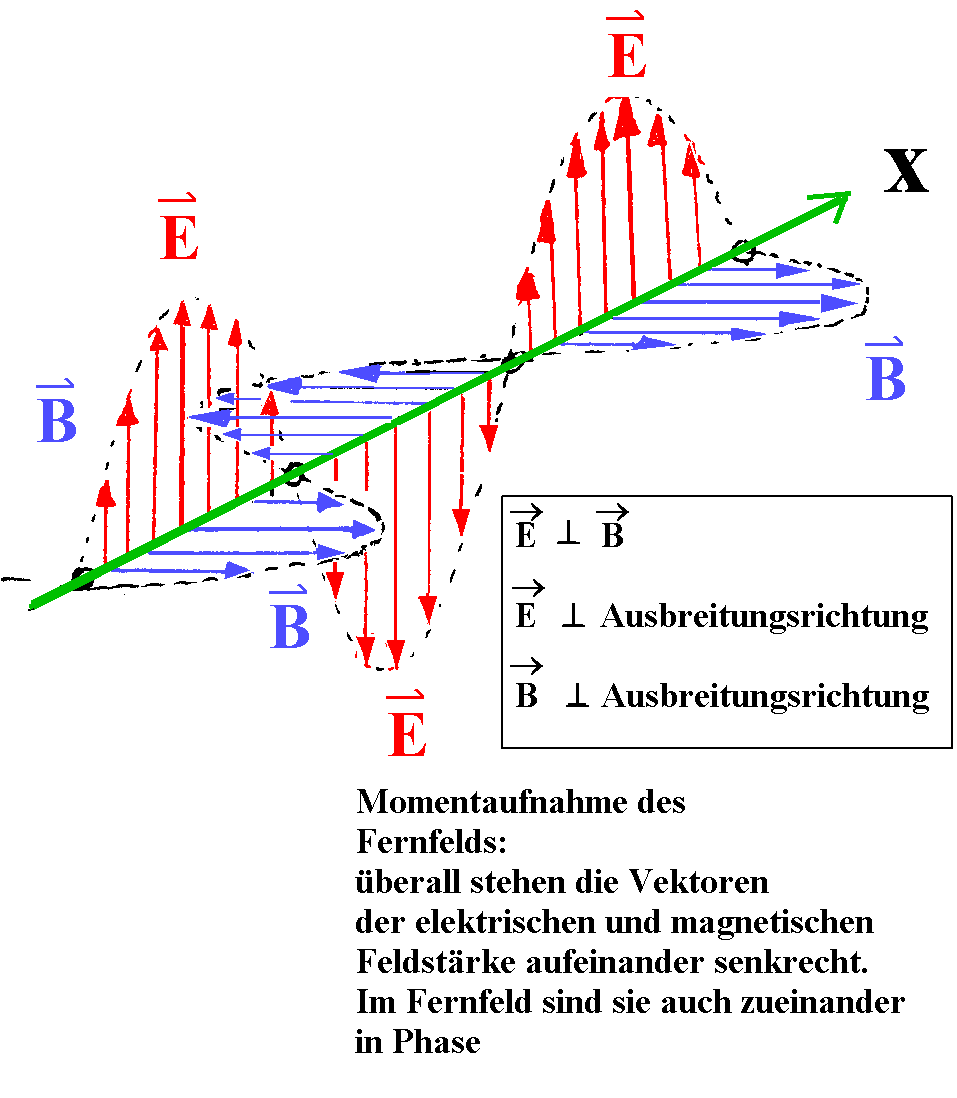Abb. 2: Ein Momentanbild vom Fernfeld für einen bestimmten Zeitpunkt. Da hier im mechanischen Sinn nichts schwingt, kann man nur Vektoren für die jeweiligen Feldstärken E und B zeichnen und die jeweilige "Einhüllende". Etwas später wird sich das ganze Bild etwas mehr in Ausbreitungsrichtung (x) verschoben haben.

Orts- und Zeitabhängigkeit beider Felder sind im Fernfeld im Idealfall sinusförmig. Deswegen lassen sie sich genauso wie mechanische Wellen als harmonische Wellen beschreiben.

Den 2. Schritt, das Induktionsgesetz, hatte schon Faraday um 1830 entdeckt. Die Maxwell'sche Ergänzung (3. Schritt) folgte um 1870 rein spekulativ auf Grund von Symmetriebetrachtungen. Wie erfolgreich diese doch sein können!

.

( Oktober 2013 )